Gjenopprette krypterte filer- Dette er et problem for et stort antall persondatabrukere som har blitt ofre for ulike krypteringsvirus. Antallet skadelig programvare i denne gruppen er svært stort og øker hver dag. Bare nylig har vi kommet over dusinvis av løsepengevarevarianter: CryptoLocker, Crypt0l0cker, Alpha Crypt, TeslaCrypt, CoinVault, Bit Crypt, CTB-Locker, TorrentLocker, HydraCrypt, better_call_saul, crittt, etc.
Selvfølgelig kan du gjenopprette krypterte filer ganske enkelt ved å følge instruksjonene som skaperne av viruset legger igjen på den infiserte datamaskinen. Men som oftest er kostnadene ved dekryptering svært betydelige, og du må også vite at noen løsepengevirus krypterer filer på en slik måte at det rett og slett er umulig å dekryptere dem senere. Og selvfølgelig er det bare irriterende å betale for å gjenopprette dine egne filer.
Måter å gjenopprette krypterte filer gratis
Det er flere måter å gjenopprette krypterte filer ved å bruke helt gratis og velprøvde programmer som ShadowExplorer og PhotoRec. Før og under gjenoppretting, prøv å bruke den infiserte datamaskinen så lite som mulig, på denne måten øker du sjansene for vellykket filgjenoppretting.
Instruksjonene beskrevet nedenfor må følges trinn for trinn, hvis noe ikke fungerer for deg, så STOPP, be om hjelp ved å skrive en kommentar til denne artikkelen eller lage et nytt emne på vår.
1. Fjern løsepengevirus
Kaspersky Virus Removal Tool og Malwarebytes Anti-malware kan oppdage forskjellige typer aktive løsepengevirus og vil enkelt fjerne dem fra datamaskinen din, MEN de kan ikke gjenopprette krypterte filer.
1.1. Fjern løsepengevare ved hjelp av Kaspersky Virus Removal Tool

Klikk på knappen Skannå kjøre en skanning av datamaskinen din for tilstedeværelse av et løsepengevirus.

Vent til denne prosessen er fullført og fjern eventuell skadelig programvare.
1.2. Fjern løsepenge ved bruk av Malwarebytes Anti-malware
Last ned programmet. Etter at nedlastingen er fullført, kjør den nedlastede filen.


Programoppdateringsprosedyren starter automatisk. Trykk på knappen når den er ferdig Kjør skanning. Malwarebytes Anti-malware vil begynne å skanne datamaskinen.

Umiddelbart etter skanning av datamaskinen, vil Malwarebytes Anti-malware åpne en liste over funnet komponenter av løsepengeviruset.
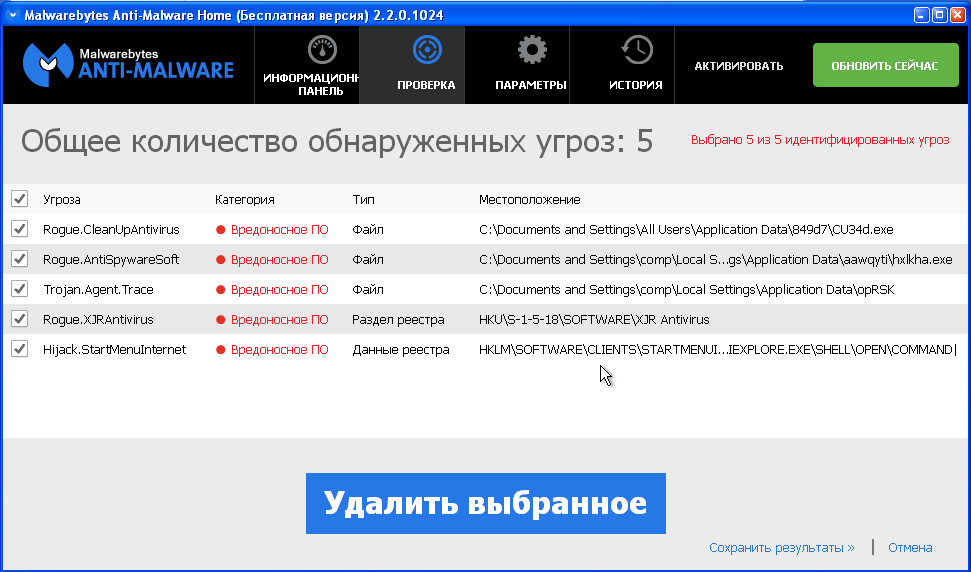
Klikk på knappen Slett valgte for å rense datamaskinen. Mens skadelig programvare blir fjernet, kan Malwarebytes Anti-malware kreve at du starter datamaskinen på nytt for å fortsette prosessen. Bekreft dette ved å velge Ja.
Etter at datamaskinen starter igjen, vil Malwarebytes Anti-malware automatisk fortsette renseprosessen.
2. Gjenopprett krypterte filer ved hjelp av ShadowExplorer
ShadowExplorer er et lite verktøy som lar deg gjenopprette skyggekopier av filer som opprettes automatisk av Windows-operativsystemet (7-10). Dette vil tillate deg å gjenopprette de krypterte filene til deres opprinnelige tilstand.
Last ned programmet. Programmet er i et zip-arkiv. Høyreklikk derfor på den nedlastede filen og velg Pakk ut alle. Åpne deretter ShadowExplorerPortable-mappen.

Start ShadowExplorer. Velg disken du trenger og datoen skyggekopiene ble laget, henholdsvis nummer 1 og 2 i figuren under.

Høyreklikk på katalogen eller filen du vil gjenopprette en kopi av. Fra menyen som vises, velg Eksporter.

Og til slutt, velg mappen der den gjenopprettede filen skal kopieres.
3. Gjenopprett krypterte filer ved hjelp av PhotoRec
PhotoRec er et gratis program designet for å gjenopprette slettede og tapte filer. Ved å bruke den kan du gjenopprette originale filer som løsepengevirus slettet etter å ha opprettet de krypterte kopier.
Last ned programmet. Programmet ligger i arkivet. Høyreklikk derfor på den nedlastede filen og velg Pakk ut alle. Åpne deretter testdisk-mappen.

Finn QPhotoRec_Win i listen over filer og kjør den. Et programvindu åpnes som viser alle partisjonene til de tilgjengelige diskene.

I listen over partisjoner velger du den som de krypterte filene er plassert på. Klikk deretter på Filformater-knappen.

Som standard er programmet konfigurert til å gjenopprette alle filtyper, men for å fremskynde arbeidet, anbefales det å la bare filtypene du trenger for å gjenopprette. Når du har fullført valget, klikker du OK.
Nederst i QPhotoRec-programvinduet finner du Bla gjennom-knappen og klikker på den. Du må velge katalogen der de gjenopprettede filene skal lagres. Det anbefales å bruke en disk som ikke inneholder krypterte filer som krever gjenoppretting (du kan bruke en flash-stasjon eller ekstern stasjon).
For å starte prosedyren for å søke og gjenopprette originale kopier av krypterte filer, klikk på Søk-knappen. Denne prosessen tar ganske lang tid, så vær tålmodig.

Når søket er fullført, klikker du på Avslutt-knappen. Åpne nå mappen du har valgt for å lagre de gjenopprettede filene.

Mappen vil inneholde kataloger kalt recup_dir.1, recup_dir.2, recup_dir.3, etc. Jo flere filer programmet finner, jo flere kataloger blir det. For å finne filene du trenger, sjekk alle katalogene én etter én. For å gjøre det lettere å finne filen du trenger blant et stort antall gjenopprettede, bruk det innebygde Windows-søkesystemet (etter filinnhold), og ikke glem funksjonen til å sortere filer i kataloger. Du kan velge datoen filen ble endret som et sorteringsalternativ, siden QPhotoRec forsøker å gjenopprette denne egenskapen når du gjenoppretter en fil.
I dag, 22.09.17, er det på tide at den fullstendige utgivelsen av mobilversjonen slippes Minecraft 1.2! Hvorfor bare Minecraft? Og ikke Minecraft PE som vi pleide å kalle det. Ja, fordi spillutviklerne bestemte seg for å endre navnet og nå er det to identiske spilltitler, en for en datamaskin, den andre for en mobilenhet. Men hvis vi ser nærmere etter, vil vi legge merke til at det er et nytt navn, som kan oversettes som "Det er morsommere sammen." Denne setningen kombinerer flere operativsystemer samtidig: IOS, Android, Windows og Xbox og Nintendo Switch.
Med utgivelsen av 1.2.0 ble det gjort mange endringer i spillet som dekker alle de gamle. Utviklerne bestemte at nå med hver nye versjon vil Minecraft være enda mer kompatibel med andre systemer.





Store endringer
- Versjon 1.2 passer veldig godt for nybegynnere, for nå før du starter spillet, må du gjennom trening.
- En bok dukket opp. I motsetning til dataversjonen kan du her lese to sider samtidig.
- En bonuskiste med nødvendige ressurser for å overleve har blitt introdusert ved starten av spillet.
- Et rustningsstativ vil dukke opp, dette er den mest etterlengtede innovasjonen.
- Dype kløfter med ressursene du trenger.
- Lyse og interessante papegøyer.
- Platespiller.
- Lagt til flagg.
- Nye prestasjoner.
I versjon 1.2.13 feil med grensesnitt, grafikk, kommandoer er fikset. Det er mange gode endringer knyttet til mobs. Vi fikset mange feil med spillingen og forbedret den mye. Rettet krasj på forskjellige enheter. Ingen flere blokk-IDer! Versjon 1.2.13 fungerer ikke på Xbox Live !
C Mail skyer Last ned Minecraft PE 1.2.13 ORIGINAL (Android 4.2+)
C Mail skyer Last ned Minecraft PE 1.2.13 ORIGINAL (X86/Android 4.2+)
C Mail skyer Last ned Minecraft PE 1.2.13 Mod (Android 4.2+)
C Mail skyer Last ned Minecraft PE 1.2.10 ORIGINAL (Android 4.2+)
C Mail skyer Last ned Minecraft PE 1.2.10 ORIGINAL (X86/Android 4.2+)
C Mail skyer Last ned Minecraft PE 1.2.10 Mod (Android 2.3.6+)
I versjon 1.2.10 Mange feil har blitt fikset, pluss flere nye små endringer har dukket opp. Stabil versjon, fungerer overalt!
Kort informasjon fra teorien
To heltall a og b er sammenlignbare modulo m, hvis når man deler med m de gir de samme restene. Antall m kalt sammenligningsmodulen.
Tilsvarende ordlyd: a og b sammenlignbar i modul m, hvis deres forskjell a–b delt på m uten rest, eller hvis en kan representeres i skjemaet a = b + k m, Hvor k- noe heltall.
For eksempel: 32 og – 10 er sammenlignbare modulo 7, siden
32 = 7 4 +4 og – 10 = 7 (- 2) + 4,
11 og 21 er sammenlignbare modulo 10, fordi (11 – 21) ,
2 10(mod8) fordi (2 – 10) 8
35 27(mod8) fordi 35 = 27 + 8 1 .
Uttalelse " a og b sammenlignbar i modul m" er registrert i
form: en b( mod m).
Egenskaper ved sammenligninger. Sammenliknbarhetsrelasjonen modulo et naturlig tall har følgende egenskaper:
- refleksivitet: for enhver helhet en rettferdig en en( mod m).
- symmetri: hvis en b( mod m), deretter b en( mod m).
- transitivitet:
Hvis en b( mod m) Og b c( mod m), deretter a c( mod m).
I kraft av disse tre egenskapene er sammenlignbarhetsrelasjonen en ekvivalensrelasjon på settet med heltall.
Alle to heltall er sammenlignbare modulo 1.
Hvis tallene : a og b sammenlignbar i modul m, det er en b( mod m) Og m delt på n, At en Og b sammenlignbar i modul n, det er en b( mod n) .
For to tall a og b var sammenlignbare i modul m , hvis kanoniske primfaktorisering er:
m = …. , i=1,2,…,d nødvendig og tilstrekkelig til
en b( mod ), i=1,2,…,d.
Hvis en b( mod m 1) og a b( mod m 2), At en b( mod m),
Hvor m = [m 1, m 2 ].
Sammenligninger med hensyn til samme modul har mange av egenskapene til vanlige likheter. For eksempel kan de legges til, trekkes fra og multipliseres:
hvis tallene a 1 , a 2 , …, en n Og b 1 , b 2 ,..., b n parvis sammenlignbare i modul m , deretter summene deres ( a 1 + a 2 +...+a n) Og (b 1 +b 2 +...+b n ) og fungerer
(en 1 en 2 … en n ) Og (b 1 b 2 … b n ) er også sammenlignbare i modul m .
Hvis tallene a og b sammenlignbar i modul m, deretter gradene deres en k Og b k også sammenlignbar i modul m under enhver naturlig k .
Eksempel. Ved å bruke denne egenskapen kan du finne rester fra å dele tall. Anta at vi må finne resten av divisjonen 1234 2327 kl. 11.
Løsning. 1234 2327 ![]() . 1234 = 11 112 +2 1234 2(mod 11), så etter eiendom får vi 1234 2327 .
. 1234 = 11 112 +2 1234 2(mod 11), så etter eiendom får vi 1234 2327 .
2 10 1 (mod 11) (2 10) 232 1 232 (mod 11) 2 2320 1 (mod 11).
Tenk nå på 2 7 = 128 = 11 11 + 7, derav 2 7 7 (mod 11).
Vi fikk 2 2320 1(mod 11) og 2 7 7(mod 11). Ved egenskapen til produktet av sammenligninger av en modul får vi:
2 2320 1 (mod 11) .
Ved å bruke transitivitetsegenskapen får vi
1234 2327 og 1234 2327),
Det vil si at resten når du deler 1234 2327 med 11 er 7.
Sammenligninger kan imidlertid ikke deles på hverandre eller med andre tall. Så hvis 14 20( mod 6) , og deretter redusere med 2, får vi en feilaktig sammenligning 7 10( mod 6) fordi (7 – 10) er ikke delelig med 6 uten en rest; eller 24 4(mod 10)→ 6 4 (mod 10), men sammenligningen 6 (mod 10) er feil.
Forkortelsesreglene for sammenligninger er som følger:
Du kan dele begge sider av sammenligningen med et tall coprime til modulen if ac bc( mod m) og ( s;m ) = 1 , Det en b( mod m).
- Du kan samtidig dele begge sider av sammenligningen og modulen med deres felles divisor: hvis ac bc( mod mс), At en b( mod m).
Du kan heller ikke utføre de angitte operasjonene hvis modulene ikke stemmer overens.
Fradragsklasser. Settet med alle tall som kan sammenlignes med en modulo m , kalles klassen av modulo-rester m og er utpekt .
Så sammenligningen en b( mod m) tilsvarende = .
Fradragssystemer. Restsystemet lar deg utføre aritmetiske operasjoner på et begrenset sett med tall uten å gå utover grensene. Komplett system med fradrag modulo m – ethvert sett med m parvis uforlignelig modul m heltall. Vanligvis som et komplett system av modulo-fradrag m de minste ikke-negative restene 0, 1, … tas. m – 1, eller de absolutt minste fradragene, bestående
fra tall 0, 1, 2,…. ved oddetall m ,
og tall 0, 1, 2,…. - 1), i tilfelle jevn m .
Det maksimale settet med parvis uforlignelig modul m tall coprime til m , kalt redusert fradragssystem modulo m . Ethvert redusert system av modulo-rester m inneholder elementer, her er Euler-funksjonen.
Eulers teorem. For alle coprimtall gjelder følgende formel: 1(mod m)
Fermats teorem. Hvis s - primtall og s deler seg ikke en , Det
![]() a (mod p)
a (mod p)
Disse teoremene brukes også til å finne rester når man deler forskjellige tall. [File mht:Forelesninger om tallteori, mine dokumenter]
Eksempel 1. Den niende potensen av et ensifret tall ender på 7. Finn dette tallet.
Løsning. a 9 º 7 (mod 10) – dette er gitt. I tillegg er det åpenbart at (7, 10)=1 og ( en, 10)=1. Ved Eulers teorem, a j (10) º 1(mod 10). Derfor en 4 º 1 (mod 10) og, etter kvadrering, en 8 º 1 (mod 10). La oss dele et 9 º 7(mod 10) ledd på ledd med en 8 º 1(mod 10) og få en º 7(mod 10). Dette betyr at a=7.
Eksempel 2. Bevis at 1 18 +2 18 +3 18 +4 18 +5 18 +6 18 º -1(mod 7)
Bevis. Tallene 1, 2, 3, 4, 5, 6 er coprime til 7. Ved Fermats teorem har vi:
La oss kube disse sammenligningene og legge dem sammen:
1 18 +2 18 +3 18 +4 18 +5 18 +6 18 º 6(mod 7) º -1(mod 7)
Eksempel 3. Finn resten når 7402 er delt på 101.
Løsning. Tallet 101 er primtall, (7, 101)=1, derfor, ifølge Fermats teorem: 7 100 º 1(mod 101). La oss heve denne sammenligningen til fjerde potens: 7,400 º 1(mod 101), multipliser den med den åpenbare sammenligningen 7 2 º 49(mod 101), vi får: 7,402 º 49(mod 101). Dette betyr at resten når du deler 7402 med 101 er 49.
Eksempel 4. Finn de to siste sifrene i 243 402.
Løsning. De to siste sifrene i dette tallet er resten av å dele det med 100. Vi har: 243=200+43; 200+43 º 43(mod 100), og for å øke den siste åpenbare sammenligningen med 402. potens, vil vi utvide venstre side ved å bruke Newtons binomiale (mentalt, selvfølgelig). I dette gigantiske uttrykket inneholder alle ledd unntatt de siste en potens på 200, dvs. er delbare med 100, så de kan ekskluderes fra sammenligningen, hvoretter det er klart hvorfor 243.402 º 43.402 (mod 100). Videre er 43 og 100 coprime, som betyr, ved Eulers teorem, 43 j (100) º 1 (mod 100). Vi teller:
j (100)= j (2 2 × 5 2)=(10–5)(10–2)=40.
Vi har en sammenligning: 43 40 º 1(mod 100), som vi umiddelbart hever til tiende potens og multipliserer ledd for ledd med den åpenbare sammenligningen, testet på en kalkulator: 43 2 º 49(mod 100). Vi får:
 |
| |
derfor er de to siste sifrene i tallet 243 402 4 og 9.
Eksempel 5. Bevis at (73 12 -1) er delelig med 105.
Løsning. Vi har: 105=3 × 5 × 7, (73,3)=(73,5)=(73,7)=1. I følge Fermats teorem:
73 2 º 1 (mod 3)
73 4 º 1 (mod 5)
73 6 º 1 (mod 7)
Ved å multiplisere får vi:
73 12 º 1(mod 3),(mod 5),(mod 7),
hvorfra det, i henhold til egenskapene til sammenligninger angitt i paragraf 16, umiddelbart følger:
73 12 -1 º 0 (mod 105),
for 105 er det minste felles multiplum av tallene 3, 5 og 7. Dette er akkurat det som var nødvendig.
Eksempel. Du må finne resten når du deler et tall på 5.
Løsning. r (mod 5).(12; 5) = 1; spor. 12 og 5 er relativt primtall, ifølge Eulers teorem 1(mod 5); = 4 1 (mod 5);
Men 2751 = 4,687 + 3;
deretter (12 4) 687 1 687 (mod 5) 12 2748 1 (mod 5) og 12 2 (mod 5) 12 3 2 3 (mod 5) Alternativ 7. 99 º 11 (mod 4); Alternativ 8. 1347
Alternativ 20. 11 203 ; Alternativ 21. 7 302 ; Alternativ 22. 6 32 .
Oppgave 4. Finn resten når du deler et tall en n til m:
Alternativ 1. 20 11, m=9; Alternativ 2. 383 175, m=45; Alternativ 3. 109 345, m=14;
Alternativ 4. 439 291 , m=60; Alternativ 5. 293 275, m=48; Alternativ 6. 93 41, m=111;
Alternativ 7. 3 80, m=11; Alternativ 8. 20 17 , m=9; Alternativ 9. 3 200, m=101;
Alternativ 10. 11 65, m=80; Alternativ 11. 7 402, m=101; Alternativ 12. 13 88, m=89;
Alternativ 13. 3 157 , m=100; Alternativ 14. 15 231 , m=16; Alternativ 15. 208 208 , m=23;
Alternativ 16. 13 88, m=89; Alternativ 17. 11 65, m=80; Alternativ 18. 66 17, m=7;
Alternativ 19. 117 53, m=11; Alternativ 20. 11 1841 , m=7;
Oppgave 5. Finn resten etter å ha delt summen på m:
Alternativ 1. 3 80 + 7 80, m=11; Alternativ 2. 3 100 + 5 100, m=7;
Alternativ 3. 2 100 +3 100 , m=5; Alternativ 4. 5 70 +7 50, m=12;
Alternativ 5. 12 1231 + 14 4324, m=13; Alternativ 6. 7 65 + 11 65, m=80;
Alternativ 7. 3200 + 7200, m=101; Alternativ 8. 5 80 + 7 100, m=13;
Alternativ 9. 5 70 + 7 50, m=12; Alternativ 10. 13 100 + 5 50, m=18;
Alternativ 11. 3 80 + 7 80, m=11; Alternativ 12. 2 100 + 3 100, m=5;
Alternativ 13. 3 80 + 7 80, m=11; Alternativ 14. 3 100 + 5 100, m=7;
Alternativ 15. 3 80 + 7 80, m=11; Alternativ 16. 3 100 + 5 100, m=7;
Alternativ 17. 2 100 +3 100 , m=5; Alternativ 18. 5 70 +7 50, m=12;
Alternativ 19. 12 1231 + 14 4324, m=13; Alternativ 20. 7 65 + 11 65, m=80;
PRAKTISK LEKSE nr. 6
Fradragssystemer
Spørsmål til leksjonen: