Funksjon er et av de viktigste matematiske begrepene. Funksjon - variabel avhengighet på fra variabel x, hvis hver verdi X samsvarer med en enkelt verdi på. Variabel X kalt den uavhengige variabelen eller argumentet. Variabel på kalt den avhengige variabelen. Alle verdier av den uavhengige variabelen (variabel x) danner definisjonsdomenet for funksjonen. Alle verdier som den avhengige variabelen tar (variabel y), danner verdiområdet for funksjonen.
Funksjonsgraf kall opp settet med alle punkter i koordinatplanet, hvis abscisse er lik verdiene til argumentet, og ordinatene er lik de tilsvarende verdiene til funksjonen, det vil si verdiene til variable er plottet langs abscisseaksen x, og verdiene til variabelen er plottet langs ordinataksen y. For å tegne en funksjon må du kjenne egenskapene til funksjonen. Hovedegenskapene til funksjonen vil bli diskutert nedenfor!
For å bygge en graf av en funksjon, anbefaler vi å bruke programmet vårt - Graffunksjoner online. Hvis du har spørsmål mens du studerer materialet på denne siden, kan du alltid stille dem på forumet vårt. Også på forumet vil de hjelpe deg med å løse problemer i matematikk, kjemi, geometri, sannsynlighetsteori og mange andre fag!
Grunnleggende egenskaper ved funksjoner.
1) Funksjonsdomene og funksjonsområde.
Domenet til en funksjon er settet med alle gyldige gyldige argumentverdier x(variabel x), som funksjonen for y = f(x) fast bestemt.
Rekkevidden til en funksjon er settet av alle reelle verdier y, som funksjonen godtar.
I elementær matematikk studeres funksjoner bare på settet med reelle tall.
2) Funksjonsnuller.
Funksjon null er verdien av argumentet der verdien av funksjonen er lik null.
3) Intervaller av konstant fortegn for en funksjon.
Intervaller med konstant fortegn for en funksjon er sett med argumentverdier der funksjonsverdiene bare er positive eller bare negative.
4) Monotonicitet av funksjonen.
En økende funksjon (i et visst intervall) er en funksjon der en større verdi av argumentet fra dette intervallet tilsvarer en større verdi av funksjonen.
En avtagende funksjon (i et visst intervall) er en funksjon der en større verdi av argumentet fra dette intervallet tilsvarer en mindre verdi av funksjonen.
5) Partall (oddelig) funksjon.
En jevn funksjon er en funksjon hvis definisjonsdomene er symmetrisk med hensyn til opprinnelsen og for enhver X fra definisjonsdomenet likheten f(-x) = f(x). Grafen til en jevn funksjon er symmetrisk om ordinaten.
En oddetallsfunksjon er en funksjon hvis definisjonsdomene er symmetrisk med hensyn til opprinnelsen og for evt. X fra definisjonsdomenet er likheten sann f(-x) = - f(x). Grafen til en oddetallsfunksjon er symmetrisk om opprinnelsen.
6) Begrensede og ubegrensede funksjoner.
En funksjon kalles begrenset hvis det er et positivt tall M slik at |f(x)| ≤ M for alle verdier av x. Hvis et slikt nummer ikke eksisterer, er funksjonen ubegrenset.
7) Periodisitet av funksjonen.
En funksjon f(x) er periodisk hvis det er et tall som ikke er null, slik at for enhver x f(x+T) = f(x). Dette minste tallet kalles funksjonens periode. Alle trigonometriske funksjoner er periodiske. (Trigonometriske formler).
Etter å ha studert disse egenskapene til en funksjon, kan du enkelt utforske funksjonen, og ved å bruke egenskapene til funksjonen kan du bygge en graf over funksjonen. Se også på materialet om sannhetstabellen, multiplikasjonstabellen, periodisk tabell, tabell over deriverte og tabell over integraler.
Funksjonsnuller
Hva er funksjonsnuller? Hvordan bestemme nullene til en funksjon analytisk og grafisk?
Funksjonsnuller- dette er argumentverdiene der funksjonen er lik null.
For å finne nullene til funksjonen gitt av formelen y=f(x), må du løse ligningen f(x)=0.
Hvis ligningen ikke har røtter, har funksjonen ingen nuller.
1) Finn nullene til den lineære funksjonen y=3x+15.
For å finne nullpunktene til funksjonen løser du ligningen 3x+15 =0.
Dermed er nullpunktet til funksjonen y=3x+15 - x= -5.
2) Finn nullene til den kvadratiske funksjonen f(x)=x²-7x+12.
For å finne nullpunktene til funksjonen, løs andregradsligningen
Røttene x1=3 og x2=4 er null for denne funksjonen.
3) Finn nullpunktene til funksjonen
En brøk er fornuftig hvis nevneren ikke er null. Derfor, x²-1≠0, x² ≠ 1, x ≠±1. Det vil si definisjonsdomenet til en gitt funksjon (DO)
![]()
Av røttene til ligningen x²+5x+4=0 x1=-1 x2=-4, er bare x=-4 inkludert i definisjonsdomenet.
For å finne nullpunktene til en funksjon gitt grafisk, må du finne skjæringspunktene til funksjonsgrafen med abscisseaksen.
Hvis grafen ikke skjærer Ox-aksen, har funksjonen ingen nuller.

funksjonen hvis graf er vist i figuren har fire nuller -
I algebra oppstår problemet med å finne nullpunktene til en funksjon både som en selvstendig oppgave og når man løser andre problemer, for eksempel når man studerer en funksjon, løser ulikheter osv.
www.algebraclass.ru
Regel for funksjonsnull

![]()
![]()
Grunnleggende begreper og egenskaper ved funksjoner
Regel (lov om) korrespondanse. Monoton funksjon .
Begrensede og ubegrensede funksjoner. Kontinuerlig og
diskontinuerlig funksjon . Partall og odde funksjoner.
Periodisk funksjon. Periode for funksjonen.
Funksjonsnuller . Asymptote .
Definisjonsdomenet og verdiområdet til en funksjon. I elementær matematikk studeres funksjoner bare på settet med reelle tall R . Dette betyr at funksjonsargumentet bare kan ta de reelle verdiene som funksjonen er definert for, dvs. den aksepterer også bare reelle verdier. En haug med X alle gyldige gyldige argumentverdier x, som funksjonen for y = f (x) er definert, kalt domene til funksjonen. En haug med Y alle reelle verdier y, som funksjonen godtar, kalles funksjonsområde. Nå kan vi gi en mer presis definisjon av funksjonen: regel (lov) av korrespondanse mellom sett X Og Y , etter hvilken for hvert element fra settet X du kan finne ett og bare ett element fra settet Y, kalles en funksjon .
Fra denne definisjonen følger det at en funksjon anses som definert hvis:
— definisjonsdomenet for funksjonen er spesifisert X ;
— funksjonsområdet er spesifisert Y ;
— korrespondanseregelen (loven) er kjent, og slik at for hver
argumentverdi, kan bare én funksjonsverdi finnes.
Dette kravet om entydighet av funksjonen er obligatorisk.

Monoton funksjon.
Hvis for to verdier av argumentet x 1 og x 2 i betingelsen x 2 > x 1 følger f (x 2) > f (x 1), deretter funksjonen f (x) er kalt økende; hvis for noen x 1 og x 2 i betingelsen x 2 > x 1 følger f (x 2) 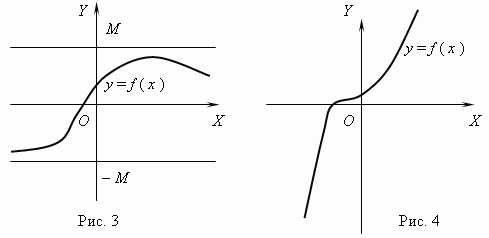
Funksjonen vist i fig. 3 er begrenset, men ikke monoton. Funksjonen i fig. 4 er akkurat det motsatte, monoton, men ubegrenset. (Forklar dette takk!).
Kontinuerlige og diskontinuerlige funksjoner. Funksjon y = f (x) er kalt kontinuerlige på punktet x = en, Hvis:
1) funksjonen er definert når x = en, dvs. f (en) finnes;
2) eksisterer avgrenset grense lim f (x) ;
Hvis minst én av disse betingelsene ikke er oppfylt, kalles funksjonen opp eksplosiv på punktet x = en .
Hvis funksjonen er kontinuerlig under alle punkter i definisjonsdomenet, da heter det kontinuerlig funksjon.

Partall og odde funksjoner. Hvis for noen x fra definisjonsdomenet til funksjonen gjelder følgende: f (— x) = f (x), så kalles funksjonen til og med; hvis det skjer: f (— x) = — f (x), så kalles funksjonen merkelig. Graf over en jevn funksjon symmetrisk om Y-aksen(Fig. 5), en graf over en oddetallsfunksjon Sim metrisk med hensyn til opprinnelsen(Fig. 6).
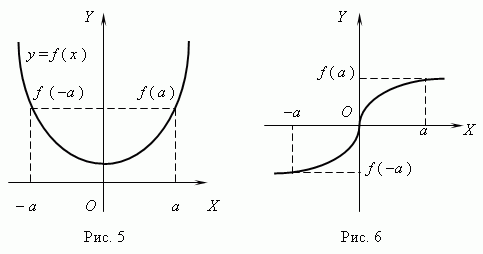
Periodisk funksjon. Funksjon f (x) — periodisk, hvis noe slikt eksisterer ikke-null Antall T til hva noen x fra definisjonsdomenet til funksjonen gjelder følgende: f (x + T) = f (x). Dette minst nummeret ringes opp funksjonens periode. Alle trigonometriske funksjoner er periodiske.
Eksempel 1. Bevis den synden x har en periode på 2.
Løsning: Vi vet at synd ( x+ 2 n) = synd x, Hvor n= 0, ± 1, ± 2, …
Derfor tillegg 2 n ikke til sinusargumentet
endrer verdien e. Er det et annet nummer med dette
La oss late som det P– et slikt tall, dvs. likestilling:
gyldig for enhver verdi x. Men så har det
sted og kl x= / 2, dvs.
synd(/2 + P) = synd / 2 = 1.
Men ifølge reduksjonsformelen synd (/ 2 + P) = cos P. Deretter
av de to siste likhetene følger det at cos P= 1, men vi
vi vet at dette er sant bare når P = 2 n. Siden den minste
ikke-null tall fra 2 n er 2, så dette tallet
og det er en periodesynd x. Det kan bevises på lignende måte at 2
er også en periode for cos x .
Bevis at funksjonene tan x og barneseng x har mensen.
Eksempel 2. Hvilket tall er perioden for funksjonen sin 2 x ?
Løsning: Tenk på synd 2 x= synd(2 x+ 2 n) = synd [ 2 ( x + n) ] .
Vi ser at det legger til n til argumentasjonen x, endres ikke
funksjonsverdi. Minste ikke-null tall
fra n er , så dette er perioden synd 2 x .
Funksjonsnuller. Argumentverdien der funksjonen er lik 0 kalles null ( root) funksjon. En funksjon kan ha flere nuller. For eksempel funksjonen y = x (x + 1) (x- 3) har tre nuller: x = 0, x = — 1, x= 3. Geometrisk null funksjon – dette er abscissen til skjæringspunktet til funksjonsgrafen med aksen X .
Figur 7 viser en graf av en funksjon med nuller: x = en , x = b Og x = c .
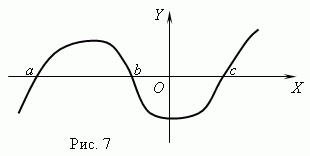
Asymptote. Hvis grafen til en funksjon på ubestemt tid nærmer seg en bestemt linje når den beveger seg bort fra origo, kalles denne linjen asymptote.
Emne 6. "Intervallmetode."
Hvis f (x) f (x 0) for x x 0, kalles funksjonen f (x). kontinuerlig ved punkt x 0.
Hvis en funksjon er kontinuerlig på hvert punkt i et eller annet intervall I, kalles den kontinuerlig i intervallet I (intervallet jeg kalles kontinuitetsintervall for funksjonen). Grafen til en funksjon på dette intervallet er en kontinuerlig linje, som de sier kan "tegnes uten å løfte blyanten fra papiret."
Egenskapen til kontinuerlige funksjoner.
Hvis funksjonen f på intervallet (a ; b) er kontinuerlig og ikke forsvinner, beholder den et konstant fortegn på dette intervallet.
En metode for å løse ulikheter med én variabel, intervallmetoden, er basert på denne egenskapen. La funksjonen f(x) være kontinuerlig på intervallet I og forsvinne ved et begrenset antall punkter i dette intervallet. Ved egenskapen til kontinuerlige funksjoner deler disse punktene I inn i intervaller, hvor den kontinuerlige funksjonen f(x) c opprettholder et konstant fortegn. For å bestemme dette tegnet er det nok å beregne verdien av funksjonen f(x) på et hvilket som helst punkt fra hvert slikt intervall. Basert på dette får vi følgende algoritme for å løse ulikheter ved hjelp av intervallmetoden.
Intervallmetode for ulikheter i formen
Intervall metode. Gjennomsnittlig nivå.
Vil du teste styrken din og finne ut resultatet av hvor klar du er for Unified State Exam eller Unified State Exam?
Lineær funksjon
En funksjon av formen kalles lineær. La oss ta en funksjon som eksempel. Den er positiv ved 3″> og negativ ved. Prikken er nullpunktet til funksjonen (). La oss vise tegnene til denne funksjonen på tallaksen:
Vi sier at "funksjonen skifter fortegn når den passerer gjennom punktet".
Det kan sees at tegnene til funksjonen tilsvarer posisjonen til funksjonsgrafen: hvis grafen er over aksen, er tegnet " ", hvis under er det " ".
Hvis vi generaliserer den resulterende regelen til en vilkårlig lineær funksjon, får vi følgende algoritme:
Kvadratisk funksjon
Jeg håper du husker hvordan du løser kvadratiske ulikheter? Hvis ikke, les emnet "Kvadratiske ulikheter." La meg minne deg om den generelle formen for en kvadratisk funksjon: .
La oss nå huske hvilke tegn den kvadratiske funksjonen tar. Grafen er en parabel, og funksjonen tar tegnet " " for de der parablen er over aksen, og " " - hvis parablen er under aksen:
Hvis en funksjon har nuller (verdier ved hvilke), skjærer parabelen aksen på to punkter - røttene til den tilsvarende kvadratiske ligningen. Dermed er aksen delt inn i tre intervaller, og fortegnene til funksjonen endres vekselvis når de passerer gjennom hver rot.
Er det mulig å bestemme skiltene på en eller annen måte uten å tegne en parabel hver gang?
Husk at et kvadratisk trinomium kan faktoriseres:
La oss markere røttene på aksen:
Vi husker at tegnet til en funksjon bare kan endres når den går gjennom roten. La oss bruke dette faktum: for hvert av de tre intervallene som aksen er delt inn i med røtter, er det nok å bestemme tegnet for funksjonen på bare ett vilkårlig valgt punkt: ved de resterende punktene i intervallet vil tegnet være det samme .
I vårt eksempel: ved 3″> er begge uttrykkene i parentes positive (erstatter, for eksempel: 0″>). Vi setter et " "-tegn på aksen:
Vel, når (erstatter, for eksempel), begge parentesene er negative, noe som betyr at produktet er positivt:
Det er det det er intervallmetode: Når vi kjenner tegnene til faktorene på hvert intervall, bestemmer vi tegnet for hele produktet.
La oss også vurdere tilfeller der funksjonen ikke har noen nuller, eller bare én.
Hvis de ikke er der, så er det ingen røtter. Dette betyr at det ikke vil være noen "passering gjennom roten". Dette betyr at funksjonen kun tar ett tegn på hele tallinjen. Det kan enkelt bestemmes ved å erstatte det med en funksjon.
Hvis det bare er én rot, berører parablen aksen, så funksjonens fortegn endres ikke når den passerer gjennom roten. Hvilken regel kan vi komme opp med for slike situasjoner?
Hvis du faktoriserer en slik funksjon, får du to identiske faktorer:
Og ethvert kvadratisk uttrykk er ikke-negativt! Derfor endres ikke funksjonens tegn. I slike tilfeller vil vi fremheve roten, når vi går gjennom som tegnet ikke endres, ved å sirkle den med en firkant:
Vi vil kalle en slik rot multipler.
Intervallmetode i ulikheter
Nå kan enhver kvadratisk ulikhet løses uten å tegne en parabel. Det er nok bare å plassere tegnene til den kvadratiske funksjonen på aksen og velge intervaller avhengig av tegnet på ulikheten. For eksempel:
La oss måle røttene på aksen og plassere skiltene:
Vi trenger delen av aksen med tegnet " "; siden ulikheten ikke er streng, er selve røttene også inkludert i løsningen:
Tenk nå på en rasjonell ulikhet - en ulikhet, der begge sider er rasjonelle uttrykk (se "rasjonelle ligninger").
Eksempel:
Alle faktorer bortsett fra én er "lineære" her, det vil si at de inneholder en variabel bare i første potens. Vi trenger slike lineære faktorer for å bruke intervallmetoden - tegnet endres når det passerer gjennom røttene deres. Men multiplikatoren har ingen røtter i det hele tatt. Dette betyr at det alltid er positivt (sjekk dette selv), og påvirker derfor ikke tegnet på hele ulikheten. Dette betyr at vi kan dele venstre og høyre side av ulikheten med den, og dermed bli kvitt den:
Nå er alt det samme som det var med kvadratiske ulikheter: vi bestemmer på hvilke punkter hver av faktorene forsvinner, markerer disse punktene på aksen og ordner tegnene. Jeg vil gjerne trekke oppmerksomheten din til et veldig viktig faktum:
Ved et partall gjør vi det samme som før: vi tegner en firkant rundt punktet og endrer ikke tegnet når vi går gjennom roten. Men i tilfelle av et oddetall, gjelder ikke denne regelen: tegnet vil fortsatt endre seg når det passerer gjennom roten. Derfor gjør vi ikke noe ekstra med en slik rot, som om det ikke var et multiplum. Reglene ovenfor gjelder for alle partall og oddetall.
Hva skal vi skrive i svaret?
Hvis vekslingen av tegn brytes, må du være veldig forsiktig, for hvis ulikheten ikke er streng, bør svaret inkludere alle skraverte punkter. Men noen av dem står ofte fra hverandre, det vil si at de ikke er inkludert i det skraverte området. I dette tilfellet legger vi dem til svaret som isolerte punkter (i krøllete klammeparenteser):
Eksempler (bestem selv):
Svar:
- Hvis blant faktorene det er enkelt, er det en rot, fordi det kan representeres som.
.
2. Finn nullpunktene til funksjonen.
f(x) ved x ![]() .
.
Svar f(x) ved x ![]() .
.
2) x 2 >-4x-5;
x 2 +4x +5>0;
La f(x)=x 2 +4x +5 så la oss finne slike x som f(x)>0,
D=-4 Ingen nuller.

4. Ulikhetssystemer. Ulikheter og ulikhetssystemer med to variabler
1) Settet med løsninger til et system av ulikheter er skjæringspunktet mellom settene med løsninger til ulikhetene som er inkludert i det.
2) Settet med løsninger til ulikheten f(x;y)>0 kan avbildes grafisk på koordinatplanet. Vanligvis deler linjen definert av ligningen f(x;y) = 0 planet i 2 deler, hvorav den ene er løsningen på ulikheten. For å bestemme hvilken del, må du erstatte koordinatene til et vilkårlig punkt M(x0;y0) som ikke ligger på linjen f(x;y)=0 inn i ulikheten. Hvis f(x0;y0) > 0, så er løsningen på ulikheten den delen av planet som inneholder punktet M0. hvis f(x0;y0)<0, то другая часть плоскости.
3) Settet med løsninger til et system av ulikheter er skjæringspunktet mellom settene med løsninger til ulikhetene som er inkludert i det. La for eksempel gis et system med ulikheter:
 .
.
For den første ulikheten er løsningssettet en sirkel med radius 2 og sentrert ved origo, og for den andre er det et halvplan plassert over den rette linjen 2x+3y=0. Settet med løsninger til dette systemet er skjæringspunktet mellom disse settene, dvs. halvsirkel.
4) Eksempel. Løs ulikhetssystemet:

Løsningen på den første ulikheten er mengden , den andre er mengden (2;7) og den tredje er mengden .
Skjæringspunktet mellom disse settene er intervallet (2;3], som er settet av løsninger til systemet med ulikheter.
5. Løse rasjonelle ulikheter ved hjelp av intervallmetoden
Metoden for intervaller er basert på følgende egenskap til binomialet (x-a): punktet x = α deler tallaksen i to deler - til høyre for punktet α binomialet (x-α)>0, og til venstre for punktet α (x-α)<0.
La det være nødvendig å løse ulikheten (x-α 1)(x-α 2)...(x-α n)>0, hvor α 1, α 2 ...α n-1, α n er faste tall, blant hvilke det ikke er like, og slik at α 1< α 2 <...< α n-1 < α n . Для решения неравенства (x-α 1)(x-α 2)...(x‑α n)>0 ved bruk av intervallmetoden fortsett som følger: tallene α 1, α 2 ...α n-1, α n er plottet på den numeriske aksen; i intervallet til høyre for den største av dem, dvs. tall α n, sett et plusstegn, i intervallet etter det fra høyre til venstre sett inn et minustegn, så et plusstegn, så et minustegn, osv. Da vil settet av alle løsninger til ulikheten (x-α 1)(x‑α 2)...(x-α n)>0 være foreningen av alle intervaller som plusstegnet er plassert i, og mengden av løsninger på ulikheten (x-α 1 )(x-α 2)...(x‑α n)<0 будет объединение всех промежутков, в которых поставлен знак «минус».
1) Løse rasjonelle ulikheter (dvs. ulikheter i formen ![]() P(x) Q(x) hvor er polynomer) er basert på følgende egenskap til en kontinuerlig funksjon: hvis en kontinuerlig funksjon forsvinner ved punktene x1 og x2 (x1; x2) og ikke har andre røtter mellom disse punktene, så i intervaller (x1; x2) funksjonen beholder fortegn.
P(x) Q(x) hvor er polynomer) er basert på følgende egenskap til en kontinuerlig funksjon: hvis en kontinuerlig funksjon forsvinner ved punktene x1 og x2 (x1; x2) og ikke har andre røtter mellom disse punktene, så i intervaller (x1; x2) funksjonen beholder fortegn.
Derfor, for å finne intervaller med konstant fortegn for funksjonen y=f(x) på tallinjen, merk alle punktene der funksjonen f(x) forsvinner eller lider av en diskontinuitet. Disse punktene deler talllinjen i flere intervaller, innenfor hver av disse er funksjonen f(x) kontinuerlig og ikke forsvinner, dvs. lagrer skiltet. For å bestemme dette tegnet er det nok å finne tegnet til funksjonen på et hvilket som helst punkt i det betraktede intervallet til talllinjen.
2) For å bestemme intervaller for konstant fortegn for en rasjonell funksjon, dvs. For å løse en rasjonell ulikhet markerer vi på talllinjen røttene til telleren og røttene til nevneren, som også er røttene og bruddpunktene til den rasjonelle funksjonen.
Løse ulikheter ved hjelp av intervallmetoden
3. ![]() < 20.
< 20.
Løsning. Utvalget av akseptable verdier bestemmes av systemet med ulikheter:
For funksjonen f(x) = ![]() – 20. Finn f(x):
– 20. Finn f(x):

hvorav x = 29 og x = 13.
f(30) = – 20 = 0,3 > 0,
f(5) = – 1 – 20 = – 10< 0.
Svar: . Grunnleggende metoder for å løse rasjonelle ligninger. 1) Det enkleste: løses ved de vanlige forenklingene - reduksjon til en fellesnevner, reduksjon av lignende termer, og så videre. Kvadratiske ligninger ax2 + bx + c = 0 løses ved...
X endres på intervallet (0,1), og avtar på intervallet = ½ [  -(1/3)
-(1/3) ], med | z|<
1.
], med | z|<
1.
b) f(z)
= - ½ [  +
+ ]
= -
(
]
= -
( ), på 1< |z|
< 3.
), på 1< |z|
< 3.
Med) f(z)
=
½ [  ]= -
½
[
]= -
½
[  ]
=
]
=
=
- ½
= -
 , med |2 - z|
< 1
, med |2 - z|
< 1
Det er en sirkel med radius 1 sentrert ved z = 2 .
I noen tilfeller kan potensserier reduseres til et sett med geometriske progresjoner, og etter dette er det lett å bestemme regionen for deres konvergens.
Etc. Undersøk konvergensen til serien
.
. . +
 +
+
 +
+
 +
1
+ ()
+ ()
2
+ ()
3
+ . . .
+
1
+ ()
+ ()
2
+ ()
3
+ . . .
Løsning. Dette er summen av to geometriske progresjoner med q 1
=
 , q 2 = () . Av betingelsene for deres konvergens følger det
, q 2 = () . Av betingelsene for deres konvergens følger det  < 1 ,
< 1 ,
 < 1 или |z|
> 1 , |z|
< 2 , т.е. область сходимости ряда кольцо
1 < |z|
< 2 .
< 1 или |z|
> 1 , |z|
< 2 , т.е. область сходимости ряда кольцо
1 < |z|
< 2 .